Understanding Legal Argument (2): Proving Facts in Law

(If you haven’t read part one, you should consider doing so now)

Recall the basic structure of legal argument

• (1) If conditions A, B and C are satisfied, then legal consequences X, Y and Z follow. (Major premise: legal rule)

• (2) Conditions A, B and C are satisfied (or not). (Minor Premise: the facts of the case)

• (3) Therefore, legal consequences X, Y and Z do (or do not) follow. (Conclusion: legal judgment in the case).

As I mentioned in part one, the first premise of this argument structure tends to get most of the attention in law schools. The second premise — establishing the actual facts of the case — tends to get rather less attention. This is unfortunate for at least three reasons.

First, in practice, establishing the facts of a case is often the most challenging aspect of a lawyer’s job. Lawyers have to interview clients to get their side of the story. They have to liaise with other potential witnesses to confirm (or disconfirm) this story. Sometimes they will need to elicit expert opinion, examine the locus in quo (scene of the crime/events) and any physical evidence, and so on. This can be a time-consuming and confusing process. What if the witness accounts vary? What if you have two experts with different opinions? Where does the truth lie?

Second, in practice, establishing the facts is often critical to winning a case. In most day-to-day legal disputes, the applicable legal rules are not in issue. The law is relatively clearcut. It’s only at the appeal court level that legal rules tend to be in dispute. Cases get appealed primarily because there is some disagreement over the applicable law. It is rare for appeal courts to reconsider the facts of case. So, in the vast majority of trials, it is establishing the facts that is crucial. Take, for example, a murder trial. The legal rules that govern murder cases are reasonably well-settled: to be guilty of murder one party must cause the death of another and must do this with intent to kill or cause grievous bodily harm. At trial, the critical issue is proving whether the accused party did in fact cause the death of another and whether they had the requisite intent to do so. If the accused accepts that they did, they might try to argue that they have a defence available to them such as self-defence or insanity. If they do, then it will need to be proven that they acted in self defence or met the requirements for legal insanity. It’s all really about the facts.

Third, the legal system has an unusual method of proving facts. This is particularly true in common law, adversarial systems (which is the type of legal system with which I am most familiar). Courts do not employ the best possible method of fact-finding. Instead, they adopt a rule-governed procedure for establishing facts that tries to balance the rights of the parties to the case against both administrative efficiency and the need to know the truth. There is a whole body of law — Evidence Law — dedicated to the arcana of legal proof. It’s both an interesting and perplexing field of inquiry — one that has both intrigued and excited commentators for centuries.

I cannot do justice to all the complexities of proving facts in what follows. Instead, I will offer a brief overview of some of the more important aspects of this process. I’ll start with a description of the key features of the legal method for proving facts. I’ll then discuss an analytical technique that people might find useful when trying to defend or critique the second premise of legal argument. I’ll use the infamous OJ Simpson trial to illustrate this technique. I’ll follow this up with a list of common errors that arise when trying to prove facts in law (the so-called ‘prosecutor’s fallacy’ being the most important). And I’ll conclude by outlining some critiques of the adversarial method of proving facts.

1. Key Features of Legal Proof

As mentioned, the legal method of proving facts is unusual. It’s not like science, or history, or any other field of empirical inquiry. I can think of no better way of highlighting this than to simply list some key features of the system. Some of these are more unusual than others.

Legal fact-finding is primarily retrospective: Lawyers and judges are usually trying to find out what happened in the past in order to figure out whether a legal rule does or does not apply to that past event. Sometimes, they engage in predictive inquiries. For example, policy-based arguments in law are often premised on the predicted consequences of following a certain legal rule. Similarly, some kinds of legal hearing, such as probation hearings or preventive detention hearings, are premised on predictions. Still, for the most part, legal fact-finding is aimed at past events. Did the accused murder the deceased? Did my client really say ‘X’ during the contractual negotiations? And so on.

Legal fact-finding is norm-directed: Lawyers and judges are not trying to find out exactly what happened in the past. Their goal is not to establish what the truth is. Their goal is to determine whether certain conditions — as set down in a particular legal rule — have been satisfied. So the fact-finding mission is always directed by the conditions set down in the relevant legal norm. Sometimes lawyers might engage in a more general form of fact-finding. For instance, if you are not sure whether your client has a good case to make, you might like to engage in a very expansive inquiry into past events to see if something stands out, but for the most part the inquiry is a narrow one, dictated by the conditions in the legal rule. At trial, this narrowness becomes particularly important as you are only allowed to introduce evidence that is relevant,/i> to the case at hand. You can’t go fishing for evidence that might be relevant and you can’t pursue tangential factual issues that are not relevant to the case simply to confuse jurors or judges. You have to stick to proving or disputing the conditions set down in the legal rule.

Legal fact-finding is adversarial (in common law systems): Lawyers defend different sides of a legal dispute. Under professional codes of ethics, they are supposed to do this zealously. Judges and juries listen to their arguments. This can result in a highly polarised and sometimes confusing fact-finding process. Lawyers will look for evidence that supports their side of the case and dismiss evidence that does not. They will call expert witnesses that support their view and not the other side’s. This is justified on the grounds that the truth may emerge when we triangulate from these biased perspectives but, as I will point out later on, this is something for which many commentators critique the adversarial system. There is a different approach in non-adversarial system. For instance, in France judges play a key role in investigating the facts of a case. At trial, they are the ones that question witnesses and elicit testimony. The lawyers take a backseat. Sometimes this is defended on the grounds that it results in a more dispassionate and less biased form of inquiry but this is debatable given the political and social role of such judges, and the fact that everyone has some biases of their own. Indeed, the inquisitorial system may amplify the biases of a single person.

Legal fact-finding is heavily testimony-dependent: Whenever a lawyer is trying to prove a fact at trial, they have to get a witness to testify to this fact. This can include eyewitnesses (people who witnessed the events at issue in the trial) or expert witnesses (people who investigated physical or forensic evidence that is relevant to the case). The dependence on testimony can be hard for people to wrap their heads around. Although physical evidence (e.g. written documents, murder weapons, blood-spattered clothes etc) is often very important in legal fact-finding, you cannot present it by itself. You typically have to get a witness to testify as to the details of that evidence (confirming that it has not been tampered with etc).

Legal Fact-Finding is probabilistic: Nothing is ever certain in life but this is particularly true in law. Lawyers and judges are not looking for irrefutable proof of certain facts. They are, instead, looking for proof that meets a certain standard. In civil (non-criminal trials), facts must be proved ‘on the balance of probabilities’, i.e. they must be more probable than not. In criminal trials, they must be proved ‘beyond reasonable doubt’. What this means, in statistical terms, is unclear. The term ‘reasonable doubt’ is vague. Some people might view it as proving someting is 75% likely to have occurred; others may view it as 90%+. There are some interesting studies on this (LINK). They are not important right now. The important point is that legal proof is probabilistic and so, in order to be rationally warranted, legal fact-finders ought to follow the basic principles of probability theory when conducting their inquiries. This doesn’t mean they have to be numerical and precise in their approach, but simply that they should adopt a mode of reasoning about facts that is consistent with the probability calculus. I’ll discuss this in more detail below.

Legal fact-finding is guided by presumptions and burdens of proof (in an adversarial system): Sometimes certain facts do not have to be proved; they are simply presumed to be true. Some of these presumptions are rebuttable — i.e. evidence can be introduced to suggest that what was presumed to be true is not, in fact, true — sometimes they are not. The best known presumption in law is, of course, the presumption of innocence in criminal law. All criminal defendants are presumed to be innocent at the outset of a trial. It is then up to the prosecution to prove that this presumption is false. This relates to the burden of proof. Ordinarily, it is up to the person bringing the case — the prosecution in a criminal trial or the plaintiff in a civil trial — to prove that the conditions specified by the governing legal rule have been satisfied. Sometimes, the burden of proof shifts to the other side. For instance, if a defendant in a criminal trial alleges that they have a defence to the charge, it can be up to them to prove that this is so, depending on the defence.

Legal fact-finding is constrained by exclusionary rules of evidence: Lawyers cannot introduce any and all evidence that might help them to prove their case. There are rules that exclude certain kinds of evidence. For example, many people have heard of the so-called rule against hearsay evidence. It is a subtle exclusionary rule. One witness cannot testify to the truth of what another person may have said. In other words, they can testify to what they may have heard, but they cannot claim or suggest that what they heard was accurate or true. There are many other kinds of exclusionary rule. In a criminal trial, the prosecution cannot, ordinarily, provide evidence regarding someone’s past criminal convictions (bad character evidence), nor can they produce evidence that was in violation of someone’s legal rights (illegally obtained evidence). Historically, many of these rules were strict. More recently, exceptions have been introduced. For example, in Ireland there used to be a very strict rule against the use of unconstitutionally obtained evidence; more recently this rule has been relaxed (or “clarified”) to allow such evidence if it was obtained inadvertently. In addition to all this, there are many formal rules regarding the procurement and handling of forensic evidence (e.g. DNA, fingerprints and blood samples). If those formal rules are breached, then the evidence may be excluded from trial, even if it is relevant. There is often a good policy-reason for these exclusions.

 

Those are some of the key features of legal fact-finding, at least in common law adversarial systems. Collectively, they mean that defending the second premise of a legal argument can be quite a challenge as you not only have to seek the truth but you have to do so in a constrained and, in some sense, unnatural way.

2. An Analytical Technique for Proving Legal Facts

Let’s set aside some of the normative and procedural oddities outlined in the previous section. If you want to think logically about the second premise of legal argument, how can you do so? As mentioned previously, legal proof is probabilistic and so it should, by rights, follow the rules of probability theory.

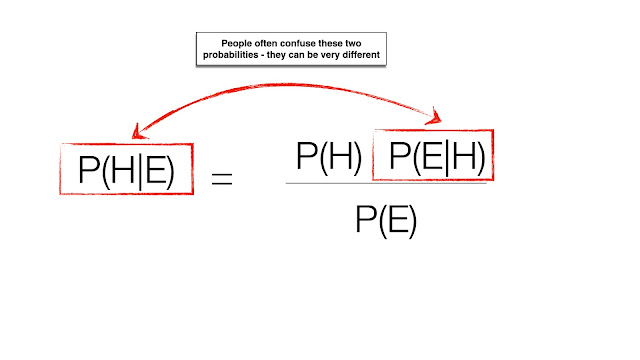
And the key rules of probability theory are, of course, capturedin Bayes’s theorem. First formulated by the Reverend Thomas Bayes in the 1700s, this theorem gives us a precise formula for working out the relative probabilities of different hypotheses (Hn) given certain evidence (En). In notational form, this is written as Pr (H|E) — where the vertical line ‘|’ can be read as ‘given’.

Bayes theorem, in its abbreviated form, is as follows:

Pr (H|E) = Pr (E|H) x Pr (H) / Pr (E)

In ordinary English, this formula says that the probability of some hypothesis given some evidence is equal to the probability of the evidence given the hypothesis (known as the ‘likelihood’ of the evidence), multiplied by the prior probability of the hypothesis, divided by the unconditional (or independent) probability of the evidence (i.e. how often would you expect to see that evidence if the hypothesis was either true or false?).

Bayes’s theorem is the correct way to reason about the probability of a hypothesis given some set of evidence. Its results can often be counterintuitive. This is mainly because of the so-called ‘base rate’ fallacy, i.e. the failure to account for prior probabilities of evidence occurring independent of the hypothesis. When we think about evidence at an intuitive level, we often ignore prior probabilities. This can lead to erroneous thinking. There are many famous examples of this. Here is one:

Cancer screening: As part of a general population mammographic screening programme, you were recently tested for breast cancer. We know from statistical evidence that 1% of all people that are routinely screened for breast cancer have cancer. We know that 80% of people that have a positive mammography actually have breast cancer (the true positive rate). We know that 9.6% of people that test positive do not (the false positive rate). You test positive. What’s the probability that you actually have breast cancer?

The answer? About 7.8%.

Many people get this wrong. Doctors who were presented with it in experimental tests tended to think the probability was closer to about 80%. This is because most people only focus on the likelihood of having a positive result if you have cancer (i.e. Pr (Positive Test | Cancer). It’s true that this is about 80% (this is the true positive rate of the test). But what about all those potential false positives and false negatives? You need to factor those in too.

In short, the problem is most people do not think in Bayesian terms. They do not calculate the probability of having cancer given a positive test result Pr (Cancer | Positive Test). If they calculated the latter, following Bayes Theorem, they would have to factor in the prior probability of having cancer and the unconditional probability of having a positive test result. Let’s do that now.

First, how probable is it that a random member of the screening population has cancer (i.e. what’s the prior probability of having cancer)? Answer: about 1/100 or 10/1000 or 100/10000. We know this because we are given this prior probability in the initial presentation of the problem.

Second, how probable is it that someone tests positive irrespective of whether they have cancer or not (i.e. what’s the unconditional probability of having a positive test)? Answer: about 10.3/100 or 103/1000 or 1030/10000. In my experience, this is the figure most people have trouble understanding. You get this by adding together the number of true positives and false positives you would expect to get in a random sample of the population. Say you test 1000 people. You would expect 10 of them to actually have cancer (1% of those screened). Of those 10, 8 will have a positive test result (this is the true positive rate). But what about the 990 other people who were screened for cancer? We know that 9.6% of them will test positive (the false positive rate). That’s about 95/1000 people. Add 8 and 95 together and you get 103. So in a random sample of 1000 people you would expect to see 103 positive test results.

If you plug those figures into Bayes’ Theorem, you get this:

Pr (Cancer| Positive Result) = (8/10) x (1/100) / (10.3/100)

Pr (Cancer | Positive Result) = 0.0776

 

Which works out at about 7.8%. (If that makes no sense to you and you want a longer explanation of this example, I recommend this explanation or this one).

Bayes Theorem is a very useful analytical tool for thinking about legal proof. In any legal case you will be trying to work out the probability that some hypothesis is true (e.g. the defendant is guilty of a crime) given some body of evidence (e.g. they were seen entering the victim’s house; their fingerprints were found on the victim’s throat etc). You will be trying to prove or disprove this hypothesis to some relevant standard of proof (balance of probabilities; beyond reasonable doubt). To think about this logically and appropriately, you should follow the Bayesian approach.

But, in practice, most lawyers and judges and juries do not do this. Why not? There are many reasons for this. Some good; some bad. Many people that work in the legal system are not comfortable with numbers or mathematical reasoning: this is often one reason why they pursued a legal career as opposed to something that demanded a more numerate style of thinking. Also, and perhaps more importantly, most of the time we do not have precise numbers that we could plug into these formulas. Instead, we have strong hunches or intuitions about the probabilities of different hypotheses and kinds of evidence. If we plug in specific numbers to the equation, these can lead to an illusion of precision or scientific rigour that is not actually present. Some court decisions have rejected probability-based proofs on the grounds of pseudo-precision. Technically, there is a school of Bayesian thought that says you can still apply the theorem without precise numbers (you can work with subjective probability estimates or ranges) but there is always the danger that this is handled badly and there is some overconfidence introduced into the process of reasoning about facts.

Fortunately, there are analytical techniques you can use that approximate a more accurate probabilistic style of reasoning and can help you to avoid some of the most common errors in probabilistic reasoning. None of these is a perfect substitute to hardcore Bayesian analysis, but they get you closer to the ideal process than working with intuitions and hunches.

One of my favourite techniques in this respect is the Heuer Table which is used widely among intelligence analysts. Intelligence analysts are often confronted with lots of different bits of evidence (surveillance footage; whistleblower reports; public statements) that they need to knit together into a coherent explanation. Sometimes analysts can leap to conclusions: dismissing security threats that are real or assuming malicious intentions that are not present. They typically do this when they latch onto a hypothesis that confers a high degree of likelihood on the available evidence. They don’t test the relative likelihood of competing hypotheses. To avoid this error, they construct a Heuer Table that lists all the available evidence, the degree of confidence they have in this evidence, and then all the potential hypothesis that could explain this evidence and the likelihood of the evidence given those hypotheses.

How might this work in law? Well, consider a famous real-world case: the OJ Simpson Trial from the mid 1990s. For those of you that don’t know, this was a trial in which the American football star OJ Simpson was charged with the murder of his ex-wife (Nicole Brown) and her friend (Ron Goldman) This was a highly contentious and complicated trial. It lasted over a year and lot of evidence was presented and disputed. I’m going to simplify things significantly for illustrative purposes. I’m going to look at a few key bits of evidence in the case from the perspective of both the prosecution and the defence.

From the prosecution’s perspective, the goal was to prove guilt beyond reasonable doubt based on a combination of physical evidence from the crime scene as well as evidence concerning Simpson’s past behaviour towards his wife and behaviour following the crime. A few bits of evidence were central to their case:

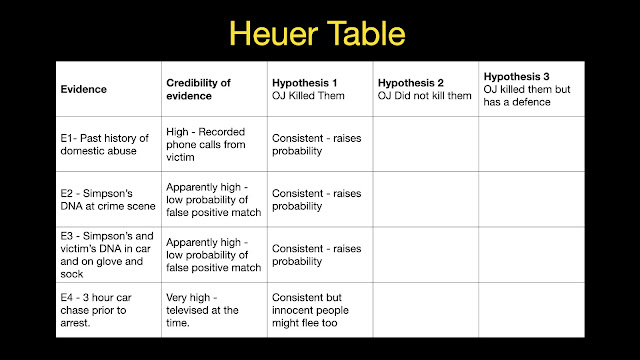
E1 - Past History of Domestic Violence: Simpson had violently abused his ex-wife in the past and the suggestion was that this violence eventually culminated in her murder.

E2 - Simpson’s DNA at the Crime Scene: Drops of blood that matched Simpson’s DNA were found in a trail leading away from the crime scene. They were small samples but the probability of accurate matches were very high.

E3 - Simpson’s DNA and Victims’ DNA in Simpson’s Car, and on Bloody Glove and Sock: Drops of blood containing the victims’ DNA and Simpson’s DNA were found in Simpson’s car (Ford Bronco), on a bloody glove found outside Simpson’s house, and on a sock in Simpson’s bedroom. The probability of accurate matches were, again, very high.

 

There was also some hair, fibre and shoeprint evidence that was less impressive, as well as some infamous post-crime incidents such as the 3-hour car chase (E4) between Simpson and the LAPD before he was arrested. Although not really a part of the prosecution’s case, this was widely publicised at the time and may have influenced anyone’s reasoning about the case, including the jury’s reasoning.

Combining this evidence together into an initial draft of the Heuer table might look something like this.

This looks like an impressive case for the prosecution. But the table is obviously incomplete because it doesn’t weigh the hypothesis of guilt against other rival hypotheses. This is where the defence’s hypothesis becomes critical.

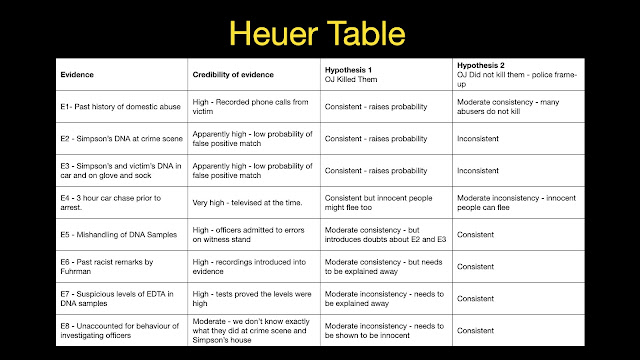
Obviously, the defence wanted to establish that Simpson was not guilty. There were, in principle, a number of different ways that they could have done this. They could have conceded that Simpson killed the victims but argued that he had some defence for doing so. For instance, perhaps he was temporarily insane or acting in self-defence. To support those hypotheses, they would have needed some evidence to support them and, to the best of my knowledge, there was none. Instead, they settled on the theory that someone else committed the crime and that Simpson was framed by corrupt and racist officers from the LAPD. This would allow them to explain away a lot of the prosecution’s case. But to make it work they would have to introduce some additional evidence to suggest that the forensic evidence introduced by the prosecution was unreliable and/or planted by the officers.

This is exactly what they did:

E5 - Mishandling of DNA Samples: The officers that collected samples from the crime scene admitted, at trial, to several mistakes in how they handled this evidence, including not changing gloves between samples and storing samples in inappropriate bags. This, the defence suggested, could have contanimated the samples significantly.

E6 - Past Racist Remarks by Mark Fuhrman: Tape recordings of one of the investigative officers suggested that he was racist and prejudiced against black people.

E7 - Suspicious or unaccounted for behaviour by the investigating officers: When the officers collected some of key bits of physical evidence from Simpson’s home, their precise movements were unaccounted for and were consistent with possible planting of evidence.

E8 - Odd levels of a preservative (EDTA) in the DNA Samples: There were suspiciously high levels of the preservative EDTA found in the DNA samples from Simpson’s home. The idea was that this was consistent with the blood samples being taken from the scene in a vial and then planted on items in Simpson’s home. This was perhaps the most technical aspect of the defence’s case.

 

When you add these bits of evidence to the Heuer table, and you consider them in light of the defence’s hypothesis (police frame-up), then you get a different sense of the case. Suddenly the prosecution is forced to explain away the new evidence either by arguing that it is an irrelevant distraction (which is essentially what they argued in relation to the racist remarks of Mark Fuhrman) or doesn’t undermine the credibility of the evidence they presented (which is what they argued in response to the criticisms of the forensic evidence). Furthermore, bear in mind that the defence did not have to prove their hypothesis beyond reasonable doubt. They just had to make it credible enough to cast reasonable doubt on the prosecution’s case. In the end, the jury seem to have been persuaded by what they had to say.

There is a lot more to be said about the Simpson case, of course. Many people continue to think he was guilty and that the result was a travesty. That’s not what’s important here. What’s important is that following Heuer technique allows you to think about the proof of legal facts in a more logical and consistent way. It is not a perfect approximation of Bayesian reasoning — it doesn’t incorporate prior probabilities effectively — but by forcing you to consider all the available evidence and assess the relative likelihood of different hypotheses, many of the basic errors of probabilistic reasoning can be avoided.

Speaking of which…

3. Common Errors in Reasoning about Facts

Humans are fallible creatures. This has always been known. But since roughly the 1970s, there has been a small cottage industry in cognitive psychology dedicated to documenting all the cognitive biases and fallacies to which humans are susceptible. Hundreds of them have now been catalogued in the experimental literature. Most of them have to do with how people respond to evidence. Many of these biases are relevant to how we think about facts in law.

It would be impossible to review the full set of experimentally documented biases in this post. Fortunately, there are some excellent resources out there that already do this. Some of them even bring order to the chaos of experimental results by classifying and taxonomising these biases. I quite like the framework developed by Buster Benson on the Better Humans website, which comes with a wonderful illustration of all the biases by John Manoogian III. What’s particularly wonderful about this illustration is that it is interactive. You can click on the name of a specific bias and be taken to the Wikipedia page explaining what it is.

As Benson suggests, there are four main types of cognitive bias:

Information filtering biases: There is too much information out there for humans to process. We need to take shortcuts to make sense of it all. This leads us to overweight some evidence, underweight other evidence and ignore some.

Narrative/Meaning biases: We want the data to make sense to us so we often make it fit together into a story or theory that is appealing to us. We look for evidence that confirms these stories, we overlook evidence that does not, and sometimes we fill in the gaps in evidence in a way that fits our preconceptions.

Quick decision biases: We do not have an infinite amount of time in which to evaluate all the data and make relevant decisions. So we often take shortcuts and make quick decisions which are self-serving or irrational.

Memory biases: Our memories of past events and past data are imperfect. They are often reconstructions based on present biases and motivations. This can lead us astray.

 

Technically speaking, not all of these biases are errors or fallacies. Sometimes they can serve us quite well and there are people that argue that they are evolutionarily adaptive: given our temporal and physical limitations it makes sense for our minds to adopt ‘quick and dirty’ decision rules that work most of the time, if not all of the time. Still, when it comes to more complex reasoning problems, where lots of evidence needs to be weighed up in order to decide what the truth is, these biases can give rise to serious problems.

I’ll discuss three major errors that I think are particularly important when it comes to the proof of legal fact.

3.1 - Errors in Hypothesis Evaluation

One of the biggest errors in legal reasoning comes when police investigators, lawyers, judges and juries evaluate hypotheses. Many times they engage in a form of motivated reasoning or confirmation bias. They first assume that a particular hypothesis is true (e.g. the suspect is guilty) and then look for evidence that confirms this hypothesis. This can lead to them overweight evidence that supports their hypothesis and discount or ignore evidence that does not fit their hypothesis.

To some extent, this kind of motivated reasoning is an intentional part of the adversarial system of legal proof. The lawyers on the different sides of the case are supposed to be biased in favour of their clients. The hope is that their opposing biases will cancel each other out and the court (the judge or the jury) can arrive at something approximating the truth. This hope is probably forlorn, to at least some extent, given that judges and juries will often themselves be guilty of motivated reasoning. They will often have their own preconceptions about the case and they will use this when weighing up the evidence.

This reasoning error can sometimes manifest itself as a formal error in how probabilistic proofs are presented in court. This happens when lawyers and triers of fact conflate the likelihood of some evidence given a certain hypothesis (Pr (Some Evidence|Hypothesis)) with the probability of the hypothesis given the same evidence (Pr (Hypothesis|Some Evidence)). As noted above, these probabilities are often very different things. For example, the probability that a defendant’s fingerprints would be found on the murder weapon, given that he is the murderer is presumably quite high (he would have needed to handle the weapon to commit the murder). But the probability that he is the murderer given that his fingerprints were found on the weapon might be much lower. There could, after all, be some innocent explanation for why he handled the weapon. Lawyers often assume that the high probability of the former implies a high probability for the latter but this is not true.

This reasoning error has been given a name that is associated with the legal system. It is called the ‘prosecutor’s fallacy’. This name is, however, somewhat unfortunate since it is not just prosecutors who make the error. Anyone who confuses different kinds of conditional probability can make it. It can happen on the defence side of a case as well.

Indeed, there is an interesting example of this error arising in the OJ Simpson case. As noted above, one element of the prosecution’s case was that OJ Simpson had a history of domestic violence and abuse against his ex-wife Nicole Brown. The prosecution suggested that this history made it more probable that he was the murderer. It was a small part of their overall case but it was part of it nonetheless.

The defence tried to rebut this argument. They claimed that the inference the prosecution was trying to draw was fallacious. This rebuttal argument was made by Alan Dershowitz. At the time of the Simpson case, Dershowitz was a well-known appeals trial lawyer with an impressive record. Since then, he has become a more notorious and dubious figure, embroiled most recently in the Jeffrey Epstein scandal. Anyway, Dershowitz claimed that the history of domestic violence was largely irrelevant to the question of Simpson’s guilt. Why so? Because only 1/2500 women who are beaten by their partners actually end up being murdered by their partners. So even if there was a history of domestic violence, it did not make it much more probable that Simpson was the murderer.

Dershowitz arrived at the 1/2500 figure by using the following statistics on crime and domestic violence. These figures came from the US circa 1992:

Population of Women in US = 125 million (approx.) 

Number of women beaten/battered per year = 3.5 million (approx.) 

Number of Women Murdered in 1992 = 4396 

Number of battered women murdered by their batterers in 1992 = 1432

 

Although we don’t know exactly how he did it, here’s one way of arriving at the 1/2500 figure:

The probability of any random woman being murdered in the US in a given year (Pr (Woman Murdered) = 4396/125 million = 0.0000394

The probability of any random woman being battered in a given year (Pr (Woman Battered)) = 3.5 million/125 million = 0.028

The probability of any random woman being murdered by a former batterer in a given year (Pr (Woman Murdered by Former Batterer)) = 1432/125 million = 0.0000114

The probability of being a woman murdered by a former batterer, given that you are a battered woman (Pr (Woman Murdered by Former Batterer|Woman Battered) = 1432/3.5 million = 0.00409 = approximately 1/2444 or (rounding up) 1/2500

 

This last probability is the one that Dershowitz mentioned in the case. On the face of it, this looks like a sophisticated piece of statistical reasoning. Dershowitz has looked at the actual figures and calculated the probability of a woman being murdered by her former batterer given that she was battered. Or, to put it more straightforwardly, he has looked at how many battered women go on to be murdered by their batterers.

The problem is that this is not the relevant probability. What Dershowitz should have calculated is the probability of being a woman murdered by your batterer given that you were murdered (Pr (Woman Murdered by Former Batterer | Woman Murdered). After all, in the Simpson case, we knew that Nicole Brown was murdered. That was not in dispute and was part of the evidence in the case. The question is whether Simpson was the murderer and whether his being a former batterer makes it more likely that he was her murderer.

This probability is very different from the one cited by Dershowitz. Although you don’t have to use Bayes’ Theorem to calculate it, it helps if you do because applying Bayes Theorem to problems like this is a good habit:

Pr (Woman Murdered by Former Batterer | Woman Murdered) = Pr (Woman Murdered | Woman Murdered by Former Batterer) x Pr (Woman Murdered by Former Batterer) / Pr (Woman Murdered)

 

You can plug the figures calculated above into this equation. Doing so, you get:

Pr (Woman Murdered by Former Batterer| Woman Murdered) = 1 x 0.0000114 / 0.0000394= 0.289 = approximately 1/3.5

 

This is obviously a very different figure from what Dershowitz came up with. Indeed, looking at it, it seems as if the prosecution’s argument was not unreasonable. Given that Nicole Brown had been murdered, the chances that she was murdered by her former batterer were reasonably high. It was not more probable than not, and certainly couldn’t be used to prove Simpson’s guilt beyond reasonable doubt. No general statistic argument of this sort could do that. But as a small part of their overall case, it was not an unreasonable point to make. (There is, of course, an easier way to arrive at this figure: divide 4396 (the total number of battered women) by 1432 (the total number of battered women who are murdered by their abusers), but it's worth going through the longer version of the calculation).

To be clear, I doubt that this probabilistic error had any major role to play in the Simpson verdict. The issue was too abstruse and technical for most people to appreciate. I suspect the defence arguments relating to police bias and forensic anomalies were more important. Still, it is a good example of how lawyers can make mistakes when evaluating the probability of different hypotheses.

3.2 - Errors in Evaluating Witness Testimony

The legal system continues to place a lot of faith in eyewitness testimony. It is often used to identify suspects and can be crucial in many trials. Furthermore, outside of eyewitnesses, the legal system depends heavily on testimony in general when proving facts.

The problems with this reliance on witness testimony have now been well-documented. There are innumerable psychological experiments suggesting that eyewitnesses often overlook or misremember crucial details of what they have witnessed. The starting point for modern research on this is probably Ulric Neisser’s tests of student recall in the aftermath of the Challenger space shuttle disaster in 1986. Neisser got his students to complete a questionnaire the day after the disaster and then tested their recall at later dates. He found that many students gave conflicting accounts in subsequent tests. Despite this, they were often very confident in the accuracy of their recall.

The problems with witness testimony are not just confined to the psychology lab. It has now been clearly demonstrated that many innocent people have been convicted on the back of faulty eyewitness evidence. The Innocence Project, which specialises in using DNA evidence to exonerate innocent prisoners, has established this over and over again. Furthermore, a 2014 report from the US National Academy of Sciences entitled Identifying the Culprit exhaustively documents many of the errors and problems that arise from the practical use of eyewitness evidence.

None of this means that eyewitness testimony should be abandoned entirely. It is still an invaluable part of the legal fact finding process. Indeed, one of the purposes of the National Academy report was to identify best practices for improving the reliability of eyewitness identification evidence.

Still, witness testimony should be treated with due care and suspicion. There are, in particular, three critical questions worth asking when you are deciding how much weight to afford witness evidence in your evaluation of the facts:

What are the witness’ motivations/interests? - Witnesses are like anyone else. They have their biases and motivations. They try to make what they saw (and what they recall of what they saw) fit their own preconceptions. They may also have more explicit biases such as a documented hatred/dislike toward an accused party or a financial interest in a certain trial outcome. Highlighting those motivations and interests can both undermine or boost their credibility. As a rough rule of thumb, it is usually more credible when a witness testifies against their own interests.

 

What are the witness’ cognitive frailties or shortcomings? - In addition to trying to make the evidence fit their own narrative, witnesses can suffer from all the general cognitive biases that afflict most human beings. They may also suffer from particular cognitive biases or frailties. Perhaps, for example, they have poor eyesight or documented memory problems. Perhaps they were intoxicated at the time of the incident. Perhaps they have a history of deception and fraud. These particular frailties will also affect the credibility of their testimony.

 

What were the ‘seeing’ conditions for the witness like? - Witnesses perceive events in a context. What was that context like? Was it one that would be conducive to them perceiving what they claim to have perceived? Did they overhear a conversation in a crowded room with lots of background chatter? Did they merely glimpse the suspect out of the corner of their eye? Was it a foggy wet morning when the accident occurred? All of these factors — and others that I cannot anticipate — will affect the credibility of the evidence they offer.

 

Finally, in an ideal world you would like to have many different witnesses, with different motivations and characteristics, to testify to the same set of facts. If the testimony of these different witnesses combines to tell a coherent story, then you can be reasonably confident that the gist of the story is true. If the testimony is contradictory and incoherent, you may have to suspend judgment. The latter would be an example of the Rashomon effect, which I have discussed in greater detail before.

This is a brief introduction to evaluating witness testimony. If you would like a longer discussion of the topic, I highly recommend Douglas Walton’s book Witness Testimony Evidence, which documents the strengths and weaknesses of this form of evidence in exhausting detail.

3.3 - Errors in Evaluating Expert Opinion Evidence

In addition to witness testimony, courts often rely on expert opinion evidence to support the fact-finding process. Most people are familiar with the role of forensic experts in criminal trials, testifying to the probative value of bloodspatters, fingerprints and DNA matches. But experts are relevant to many other trials. Doctors frequently present evidence regarding the seriousness of injuries in negligence cases, accountants testify with respect to dodgy bookkeeping practices in fraud cases, social workers and psychologists will present evidence regarding a child’s welfare in custody hearings, and so on.

The reliance on expert evidence is an exception to the usual rule against opinion evidence. Ordinarily, someone can only testify in court as to what they have seen or heard, not what they think or hypothesise might be true. Experts can do this on the assumption that their expertise allows them to make credible inferences from observed facts to potential explanations for those facts.

There are many things that can go wrong with expert evidence. In my opinion, one of the best books on this topic in recent years is Roger Koppl’s Expert Failure, which is not only an interesting review of the history of expert evidence and expert failure, but also presents a theory as why expert failure happens and what we can do about it. You may not agree with his solutions — Koppl is an economist and favours ‘market design’ solutions to the problem — but his discussion is thought provoking.

Even if you don’t read Koppl’s book, there are a handful of critical questions that are worth asking about expert evidence:

What are the expert’s biases and motivations? - Experts are just like everyone else insofar as they will have biases and motivations that can affect their testimony. They may have their pet theories that they will defend to the hilt. In the adversarial system, they are likely to be a ‘hired gun’ that will support whichever side is paying them. One of the most notorious examples of this ‘biased expert’ problem in recent history was Dr James Grigson (aka Dr Death) who testified in over 167 death penalty cases in the US. He always testified that the defendants in these cases were 100% likely to commit similar offences again in the future. He sometimes did this without interview the defendant’s himself but simply from their medical records. No credible expert could be that certain about anything.

 

What is the error rate of the test they are applying (if any)? - If the expert is applying a forensic test of some sort (e.g. fingerprint match, ballistics test etc), then what is the known error rate associated with that test? As we saw above with the cancer test example, the error rates can make a big difference when it comes to figuring out how much weight we should attach to the results of a test. In criminal law, in particular, given the presumption of innocence, it is often felt that tests with high false positive rate (i.e. tests that a falsely incriminating) should be treated with some suspicion.

 

If the evidence for a test/theory is based on experimental results, how ecologically valid were those experiments? - Scientists often test their techniques in lab conditions that have little resemblance to the real world. One of the examples of this that I have studied in detail in the past are the experimental tests for lie detection/guilty knowledge evidence. Many of the lab tests of these techniques do not resemble the kinds of conditions that would arise in a real world investigation. Experimental subjects are asked to pretend that they are lying and often don’t face any potential consequences for their actions. Many researchers are aware of this problem and try to create better experiments that more closely approximate real-world conditions. As a general rule of thumb, the closer the experimental test is to real world conditions, the better. If there are field tests of the technique, then that is even better still.

 

Are there any institutional biases/flaws to which this expert’s opinions might be susceptible? — In addition to being hired guns, experts may be susceptible to biases or flaws that are inherent to the institutions or communities in which they operate. Recent scandals in biomedical and psychological research have highlighted some of the problems that can arise. Published data is often biased in favour of positive results (i.e. experiments that prove a hypothesis or claim) and against negative results; very few academic journals publish replications of previous experiments; very few academics are incentivised to replicate or rigorously retest their own theories. Things are getting better, and there are a number of initiatives in place to correct for these biases, but they are, nevertheless, illustrative of the problems that can arise. Lawyers and judges should be on the look out for them.

 

I should close by saying that some legal systems now adopt formal reliability tests when it comes to admitting expert evidence at trial. These reliability tests force lawyers and judges to ask similar question to the ones outlined above (often adding question about whether the expert’s testimony is relevant to the case at hand, whether it coheres with the common opinion in their field, and the nature of the expert’s qualifications). My sense is that these tests are welcome but can sometimes be treated as a box-ticking exercise. Merely asking these questions is not a substitute for critical thinking. You have to assess the answers to them too.

4. Conclusion - Is Legal Fact-Finding Hopelessly Flawed?

This has been a brief review of some of the procedural features of legal fact-finding and some of the basic errors that can arise during the process. There is a lot more that could be said. I want to wrap up, however, by offering some critical reflections on the fact-finding process. In the early 1800s, Jeremy Bentham wrote a scathing critique of legal fact-finding, arguing that the procedural constraints introduced by the courts prevented them from uncovering the truth. They should, instead, adopt a system of ‘free’ proof, focused on getting at the truth, unconstrained by these rules.

Bentham specialised in scathing critiques, but others have taken up this cause since then. The philosopher Larry Laudan wrote a book called Truth, Error and Criminal Law which argued that many of the procedures and exclusionary rules adopted by the US courts are irrational or a hindrance to getting at the truth. Similarly, the philosopher Susan Haack has also developed critiques of adversarialism and exclusionary rules.

I’m torn when it comes to these critiques. There certainly are problems with legal fact-finding. The adversarial system is supposed to a wonderful machine for getting at the truth: with competing lawyers highlighting the flaws in the opposing side’s arguments, the court can eliminate errors and get closer to the truth. But whether the system lives up to that ideal in practice is another matter. The adversarial system often compounds and amplifies social inequalities. Poor, indigent defendants cannot afford good lawyers and hence see their cases wither in front of the prosecution’s better resources. Contrariwise, rich defendants (like OJ Simpson) can employ an army of lawyers that can overwhelm a poorly-financed public prosecutor. The end result is that money wins out, not the truth. Countries that have well-resourced systems of public legal aid (as Ireland and the UK once did) can correct for these weaknesses in the adversarial system. But it can be hard to maintain these systems. There are very few votes in providing resources to those charged with criminal offences.

Likewise, when it comes to exclusionary rules of evidence, there are often good rationales behind them. We don’t want the police to abuse their power. We don’t want to give them the freedom to collect any and all evidence that might support their hunches without respecting the rights of citizens. That’s why we exclude illegally obtained evidence. Similarly, we don’t want to admit evidence that might be unfairly prejudicial or that might be afforded undue weight by a jury. That’s why we exclude things like bad character evidence in criminal trials or (on the opposite side) evidence of past sexual behaviour in rape/sexual trials. But there is no doubt that these exclusionary rules sometimes have undesirable outcomes. Clearly guilty criminals can get off on technicalities (the wrong date on a search warrant) and evidence that is relevant to a case has to be ignored.

But even though the system of legal fact-finding has its weaknesses, we must bear in mind that all human systems of fact-finding have weaknesses. The reproducibility crisis in biomedicine and psychology is testament to this, as are the cases of experts leading us awry, which are documented in books like Roger Koppl’s Expert Failure.

In the end, my sense is that reform of the legal system of fact-finding is preferable to radical overhaul.

Subscribe to the newsletter