If we are to take religious believers seriously, then miracles really do happen. Indeed, several of the world’s leading religions are founded on miracle claims. Christianity is probably the most famous example of this, with the testimony concerning Jesus’s death and bodily resurrection being central to that religion’s origin. But given that we are separated from that alleged miracle by almost two thousand years (if we take the historical consensus seriously, then Jesus died around 30 CE), how can we have any confidence in its occurrence? All we have are a handful of indirect written reports, none from an actual eyewitness to the event, though several claiming to be founded on the testimony of eyewitnesses. To me, at any rate, this seems like a thin reed upon which to hang the eternal fate of one’s soul.
But suppose we did have direct eyewitness testimony of the resurrection. Suppose (per Paul’s letter to the Corinthians) we have 500 eyewitnesses all testifying to its occurrence. Should we believe them? David Hume famously argued that we shouldn’t. In his essay ‘Of Miracles’ he argued that it is only in exceptional circumstances that we would have reason to believe in miracles on the basis of eyewitness testimony. I have covered the exact details of Hume’s argument in several previous articles. I won’t rehash them here. The gist of his view is that, given the general improbability of a miracle, and given the known unreliability of eyewitness testimony (people are known to lie or misinterpret or delude themselves as to what really happened), we would only have reason to believe in a miracle, on the basis of eyewitness testimony, if the falsity of the eyewitness testimony is more improbable than the miracle itself.
The debate about Hume’s argument has become increasingly sophisticated and mathematised over the years. One cadre of critics — including Charles Babbage, Rodney Holder and John Earman — have taken issue with the application of Hume’s argument to cases involving multiple independent witnesses. They’ve argued that if you have a sufficient number of independent witnesses, then no matter how low a prior probability you assign to the occurrence of a miracle, it is possible to drive the posterior probability of the miracle’s occurrence arbitrarily high by increasing the number of witnesses.
There is a formal proof of this critique, but it is relatively intuitive. Suppose you did have 500 hundred genuinely independent witnesses (i.e. they haven’t colluded with one another or been influenced by one another) and suppose each individual witness is more likely (even if only marginally) to be telling the truth about what they saw than not. Suppose then that when you talk to them, they all say the same thing: they once saw a dead guy and then saw him alive again. In such a case, even if you were really sceptical at the outset, you’d be hard pressed to retain your scepticism by the end. The improbability of them all getting it wrong will surely be greater than the improbability of the miracle. As Babbage puts it in his critique of Hume:
[I]f independent witnesses can be found, who speak truth more frequently than falsehood, it is ALWAYS possible to assign a number of independent witnesses, the improbability of the falsehood of whose concurring testimony shall be greater than that of the improbability of the miracle itself.
(Babbage - The Ninth Bridgewater Treatise)
This would seem to scupper Hume’s argument since most religious miracle claims purport to be based on the testimony of multiple witnesses. Reasoning of this sort is what led John Earman to conclude that Hume’s argument was an ‘abject failure’ in his 2000 book Hume’s Abject Failure. But is this actually fair? It turns out that the devil is in the detail. What Babbage et al argue is correct in the case of independent witnesses, but it turns out that it is pretty difficult to achieve genuine independence. Indeed, it’s likely that there is no real world case that actually meets the formal requirements of independence. Consequently, Hume’s argument retains some relevance to this day.
This is what Arif Ahmed argues in his 2015 paper ‘Hume and the Independent Witnesses’. Ahmed’s paper is quite technical, peppered with Bayesian equations and proofs. What I’m going to try to do in this post is provide a simple, non-technical explanation of the argument it contains. In developing this non-technical explanation, I’ve drawn heavily from the paper itself and an interview that Ahmed did about its contents. I found watching/listening to the latter helped when I went back into the paper itself. So much so that I’ve embedded the video at the end of this post.
Anyway, Ahmed’s critique hinges on two problems with establishing independence. Let’s go through them both.
1. The Difficulty of Attaining True Independence
The first problem for the many witnesses objection is the practical difficultly of proving that witnesses are truly independent. By ‘true independence’ I mean a scenario in which the every eyewitness is causally sealed off from every other eyewitness in such a way that you can plausibly rule out the possibility that they have colluded with one another to get their stories straight, or that they have been directly or indirectly influenced by what another witness has said in such a way that they reinterpret what they saw, or pretend that they saw something when they really did not.
The inability to prove true independence turns out to be a big problem when it comes to the real world evaluation of witness testimony. It’s something that lawyers and police officers grapple with all the time. If I say I saw someone dressed in clown mask, running away from the jewellery store, clutching a bunch of diamond necklaces, then you might be more inclined to say that you saw the same thing, even though you really didn’t see what the person was wearing, and only saw them out of the corner of your eye. We are all subject to subtle and not so subtle forms of social influence that contaminate our testimonies. Some of us might retain our independence in the face of external influence but, as Ahmed puts it, some of us might be ‘falsehood suggestible’ (i.e. inclined to modify our testimony to cohere with the false testimony of others) and some of us might be ‘falsehood counter-suggestible’ (i.e. inclined to modify our testimony to go against the consensus view out of contrarianism). Unless you could single out the suggestible witnesses and remove them from the pool of witness, or unless they perfectly counterbalanced one another, their presence within the pool of witnesses would undermine the credibility of the total pool of witness testimony. You could no longer be confident that the improbability of falsehood was less than the improbability of a miracle.
Ahmed doesn’t spend much time on this problem of establishing true independence in his paper. He focuses more on another kind of independence (namely: conditional or formal independence). We’ll turn to that in the next section. But the difficulty of establishing true independence is something that Earman himself admits, and that Peter Millican has made much of in his criticisms of Earman’s work. As Millican explains:
Without contesting Earman’s technical results, one can dispute the seriousness of [the many witnesses objection] since most of his discussion seems to ignore entirely the epistemological dimension of how one could possibly know that the witnesses in question are genuinely independent.
(Millican 2013)
And the reality is that in the case of something like the eyewitness testimony to Jesus’s resurrection, we do have reason to doubt the true independence of the testimony that is adduced. For starters, we don’t actually have five hundred independent eyewitness reports. All we have is Paul’s claim that there were five hundred witnesses - that’s one report not multiple reports. And likewise the four Gospels are not entirely independent of one another. We know that they were written in a chronological sequence (from Mark to John) and that later gospel writers were influenced by earlier gospel writers (and by a pre-existing oral tradition). So we have reason to suspect that the actual pool of witness reports that we actually have is contaminated in such a way that we cannot be certain of true independence. This is likely to be the case with many other real-world cases of witness testimony.
2. The Difficulty of Attaining Conditional Independence
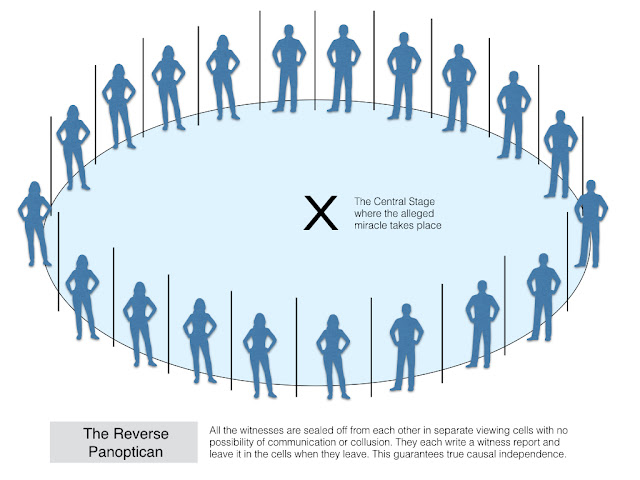
The second problem for the many witnesses objection is more technical and formal. It starts by trying to concede as much as possible to the objection and trying to conjure up a case in which we can be really confident that the witnesses have not causally influenced each other. Ahmed has a nice thought experiment that allows for this. It is based on a reversal of Jeremy Bentham’s famous Panopticon design for a prison. In Bentham’s Panopticon you have a circular array of prison cells that can all be viewed by a single guard from a central watchtower. The prisoners are, consequently, under constant threat of surveillance. Imagine if you flipped that design so that you have hundreds of hermetically-sealed viewing cells all looking at a central stage or platform upon which some, alleged, miracle is performed. That might allow for true independence. I’ll leave Ahmed explain the idea:
The Reverse Panopticon Thought Experiment: "[R]eplace the observation platform with a large stage that can be seen from each cell; but still no cell communicates with any other. Some self-proclaimed prophet has forecast a miracle on this stage at a specific date and time. In each cell we place a witness possessed of scepticism, integrity, sincerity, and general good sense; the witnesses have never been in direct or mediated contact of any sort. In each cell are a pencil and a pad. We ask each witness to observe the stage at the time in question, to write down what happened on it, and then to depart leaving the report in the cell, which automatically locks behind her. We later collect the reports, and it turns out that each one is to the effect that a man weighing about 150lbs walked across the surface of a large tank of liquid water without any other means of support."
(Ahmed 2015, 1024)
This set-up would seem to allow for the true causal independence of the witnesses. There is no possibility of them colluding with one another in the drafting of their testimony. Their reports would be uncontaminated by social influences. Could we then be confident that a miracle really occurred?
Ahmed says ‘no’. The reason for this is that even in such a case the witness testimony would not be genuinely independent. It would fail to be conditionally or formally independent. This is where things get a little bit technical. There are two formal conditions of independence that the testimony would have to meet in order for the many witnesses objection to work. These conditions don’t have to do with the causal relations between the pool of witnesses but, rather, the formal relation between the testimony and your degree of belief in the testimony (at least that’s how I understand it: the kind of independence in question is one that is conditional on your beliefs). The two conditions are:
Independence of True Positives (ITP): If you know that the miracle did occur, then no amount of (true) positive testimony to that effect from a sequences of witnesses (W1…Wn) should increase or decrease your confidence that the next witness’ (Wn+1) testimony will be positive.
Independence of False Positives (IFP): If you know that the miracle did not occur, then no amount of (false) positive testimony to that effect from a sequence of witnesses (W1…Wn) should increase or decrease your confidence that the next witness’ (Wn+1) testimony will be positive.
It might be difficult to wrap your head around these two conditions. After all, they ask you to project yourself into a situation that you are clearly not in. The whole point is that we don’t know whether the miracle occurred or not, and that we are using the testimony to establish what we should believe. And yet to understand these conditions you have to suppose that you do know whether it occurred or not. This seems odd. But the point here is that these are purely formal conditions of independence and they apply even if you do know what the reality is. The basic point that both conditions make is that witness testimony should be uncorrelated given that the miracle has/has not occurred. And, for what it is worth, Earman accepts that both conditions need to be met for the multiple witnesses objection to apply to Hume’s argument.
The problem is that they are unlikely to be met, even in a case like the reverse panopticon thought experiment. Why is this? The issue is that when you are assessing the validity of a hypothesis, given some eyewitness testimony, you are unlikely to be assessing that hypothesis in isolation from all other hypothesis. There are other hypothesis in the mix too. In the reverse panopticon case, we can suppose that there are two main hypotheses on the table (there could be more and the argument would still apply): (i) that there was a genuine miracle (i.e. someone really did walk on water) and (ii) that there was a really good magic trick/illusion (i.e. that it was only made to look like someone did). When assessing the eyewitness testimony, both hypotheses will be affected by a continuous stream of testimony to the effect that a miracle occurred, such that conditional independence does not hold true.
Think about it like this. Suppose you were the one who actually appeared to walk on the water so you know for sure whether it was an illusion or a genuine miracle. Suppose it was an illusion and you go and investigate all the eyewitness reports. The first report suggests that a genuine miracle took place. What would this do to your beliefs? Well it would probably convince you that the illusion you just performed was good enough to fool one person and so your confidence (credence) in the next eyewitness report claiming that a genuine miracle took place, would increase slightly. In other words, you’ll be more likely to think that the illusion fooled the next person. This process would continue as you proceeded through the evidence, raising your confidence that the next report will be positive concerning the occurrence of the miracle, and thereby confirming your belief that you performed a really good illusion. The IFP condition would not be met in this case. The same thing would happen if it was a genuine miracle. In that case, every time you examined an eyewitness report claiming that a genuine miracle took place you would become more convinced that the next report would say the same thing. The ITP condition would not be met in this case.
The general phenomenon at play here is something that Ahmed calls true positive and false positive ‘projectibility’. In any pool of human eyewitness testimony, the presence of a stream of true positive testimony to the effect that an event E occurred is likely to increase your confidence that the next bit of testimony will also give a true positive report; and, likewise, the presence of a stream of false positive testimony to the effect that E occurred is also likely to increase your confidence that the next bit of testimony will also give a false positive report.
This creates a major problem when it comes to assessing a pool of causally independent eyewitnesses when you don’t know whether the event to which they are testifying actually occurred. Go back again to the reverse panopticon case. Suppose you don’t know whether a genuine miracle or a really good illusion took place. You weren’t involved in the event at all. The only thing you have to go on is the eyewitness testimony. Suppose, further, that since you are a sceptic about miracles, your prior probability is that it is more likely (even if only marginally) that an illusion took place. Now, as you examine the pool of uniformly positive eyewitness testimony, something interesting will happen. Your confidence that a genuine miracle took place will go up (since that is consistent with uniform positive testimony) but so too will your confidence that a really good illusion took place (since that is also consistent with uniform positive testimony). In fact, your confidence in the latter will increase more since it started out slightly ahead. Ahmed refers to this, somewhat awkwardly, as the ‘speed’ at which you increase your credence in the relevant hypotheses: your credence in the illusion will go up faster than your credence in the miracle.
So, because true positive and false positive projectibility undermine conditional independence, and because you start off from a marginally sceptical position about the truth of a miracle given some eyewitness testimony, the existence of many witnesses, all testifying to the occurrence of a miracle, should not, by itself, cause you to believe in the occurrence of the miracle — at least not in the typical case. This means that the many witnesses objection fails, even when we imagine a highly unrealistic scenario in which we can guarantee true (causal) independence among the witnesses.
3. Some Qualifications and Limitations
That’s the ‘ordinary language’ explanation of Ahmed’s argument. There is a more formal proof in the original article. But the proof is only as good as the assumptions underlying it and there are a number that ought to be emphasised because they highlight some important limitations to the argument.
The first is that the argument is a Bayesian one, i.e. it is about the subjective probabilities you should attach to the belief in the miracle, not about the actual objective probability of the miracle’s occurrence. This is an obvious enough limitation: we can’t really assign objective probabilities to miraculous events. But because the argument is about subjective probabilities, its implications would actually change depending on the subjective prior probability you attach the likelihood of a miracle occurring. If you are someone who thinks it is more likely that a miracle occurred than (say) a really good illusion, then the projectibility of the testimony would lead you to favour the belief in the miracle’s occurrence over the belief in the really good illusion. In other words, it matters which belief starts out ‘ahead’ in your subjective probability distribution.
This, however, isn’t a very serious limitation. As Ahmed points out, Hume’s original argument was only supposed to apply to those who are marginally sceptical about the occurrence of miracles. He was asking whether testimony would ever be enough to shift that sceptic from their position of doubt. If you are already inclined to believe in miracles, then, of course, more testimony is likely to increase the subjective probability you attach to their occurrence. But, even still, Ahmed suggests that for any given miracle claim, the typical religious believer, should really start out as a marginal sceptic in its actual occurrence. After all, the whole point about miracles is that they are very rare, and that it is more likely that a claim is false than that it is true. People make miracle claims all the time, and more importantly people from different religions make them all the time; the typical religious believer is usually only willing to accept a small subset of those claims.
The second limitation is that the argument only applies to cases in which the testimony all relates to the same event and comes from the same source or origin. This is why the set-up of the reverse panopticon thought experiment is important. In that case, all the witnesses are looking at and reporting on the same event. This means the reports that you read can be genuinely compared with one another for consistency. It also means that they don’t each provide a different kind of evidence for the same event: they are all just more of the same thing. If instead of having multiple independent eyewitness reports, you had multiple independent types of evidence, then the situation would be rather different. The pool of evidence wouldn’t have the property of projectibility that was outlined above. In that case, one of the multiple lines of evidence might ‘knock out’ one of the hypotheses that is consistent with eyewitness testimony, and not another. This might result in more confidence being attached to the remaining hypothesis. This is true if the eyewitness testimony is of a different type as well. For example, if instead of all the witnesses looking at the stage upon which the person walks on water, some of them are involved in setting up the stage and didn’t see any obvious trickery, and some were positioned underneath and above the water tank and couldn’t see any trickery, then you might (and I emphasise might since all that testimony could still be consistent with an illusion) have more reason to believe that a miracle actually occurred.
This second limitation is not surprising and is, actually, quite intuitive. In science and law we already accept that it is better to have multiple different kinds of evidence converging on the same result. For example, in a murder case, it is much more likely that someone committed a murder if you find their DNA at the scene, the murder weapon with the victim’s DNA in their house, and you have multiple eyewitnesses seeing them leave the scene of the crime, than if you only have one of those types of evidence. For example, you could have multiple different labs testing the DNA evidence from the crime scene, but no matter how many reports you get back confirming that it was indeed the suspect’s DNA that was found at the crime scene, it wouldn’t make it more likely that the suspect committed the murder, if it turned out they had a perfectly good alibi explanation for why their DNA is at the crime scene.
In fact, Ahmed thinks that one of the strengths of his argument is that it explains why multiple different lines of evidence are a good thing. As he points out, it is something of a puzzle, on Bayesianism, why having multiple different kinds of evidence is better than have multiple different versions of the same kind of the evidence. After all, if each bit of evidence raises the posteriori probability of a given hypothesis, it shouldn’t really matter where it came from. The projectibility phenomenon helps to explain why this is actually a problem.
Despite its limitations, Ahmed’s argument is still pretty neat. It shows just how difficult it is to have genuinely independent witnesses. They don’t just have to be causally independent from one another; they also have to be conditionally independent. It’s very unlikely that any real world case, involving testimony to a miracle, will satisfy both kinds of independence. What’s more, the argument applies more generally to any case in which you have multiple different versions of the same kind of evidence, and at least two hypotheses that are consistent with that evidence, one of which has a higher prior probability than the other. It’s not just about eyewitness testimony. In the limit, it could apply to the evidence from your own senses or the evidence from some external detection device. Ahmed discusses this in the video below. And I’ll leave you now to watch it if you so desire.



Is this basically the same reasoning its so hard to prosecute a cop in America for murdering a black kid?
ReplyDelete