Enoch on The Epistemological Challenge to Metanormative Realism (Part 3)

Tweet

David Enoch, on the left

This post is part of a short series on David Enoch's article "The Epistemological Challenge to Metanormative Realism". Parts one and two are available here and here.

In the previous part, we outlined the precise nature of the epistemological challenge facing non-natural ("Robust") moral realists. We can briefly restate it as follows:

• Robust realists think that there is some coincidence between our moral beliefs and moral truth. They owe us some explanation of how this could be the case given that, by their own lights, moral truths are independent of our judgments and are causally inert.

In this part, we will see how Enoch responds to the challenge.

He starts with some methodological points.

1. The Plausibility Game

As outlined above, the challenge is an explanatory one. But there is a problem with this: there could be brute, unexplainable facts. There is certainly no obvious logical contradiction in the notion of a brute fact. Given this possibility, robust realism's lack of an explanation for the coincidence simply deducts a few plausibility points from the overall theory. It may still win the plausibility game.

That said, robust realists shouldn't shirk the challenge. If they can provide an explanation, and if their theory is more plausible than alternatives, it would be all the better. And when looking for an explanation we follow the standard rules of the explanation game: we try to satisfy a set of explanatory criteria and we compare and contrast competing explanations.

Three additional points need to be made about the kind of explanation we are looking for.

First, Enoch thinks that it is important to bear in mind that the coincidence between our moral beliefs and moral truth is not all that striking. No moral realist thinks that we always get things right or that our intuitions are infallible. They would agree that sound moral reasoning requires special training and sensitivities. (Note that the same is true for mathematical Platonists.) And because the correlation is weak, a relatively weak explanation is all that is required.

Second, we must accept the possibility that an fallible reasoning mechanism could become more refined and accurate in its judgments over time, e.g. by eliminating inconsistencies, increasing coherence, drawing analogies and so on. There could even be some evolutionary story about how, say, the more primitive primate reasoning mechanism was refined into the more sophisticated homo sapiens mechanism. Could the same not be true of the portion of the reasoning mechanism responsible for moral judgments?

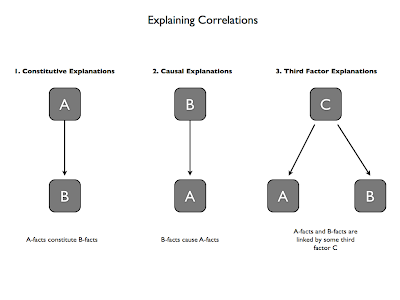
Third, there are two traditional ways to explain a correlation between two sets of facts. First, we can say that all B-facts are constituted by A-facts. Second, we can say that all B-facts are (causally) responsible for A-facts. Obviously, neither of these approaches is an option when it comes to robust realism.

However, there is another possibility: a third factor explanation. In other words, an explanation that shows how A-facts and B-facts are linked by a third factor C that is responsible for both A-facts and B-facts. Pre-established harmony explanations are of this sort, and Enoch wants to offer a pre-established harmony explanation for the troubling coincidence.

2. Survival as a Moral Good
Enoch's explanation is roughly as follows.

Let's begin with some assumptions about what is or is not a moral good (or, more generally, a moral truth). For example, let's assume that pain is morally bad and pleasure is morally good (not always and everywhere, but for the most part). Let's further assume that survival and reproduction are, in some sense, moral goods. This may be because they are correlated with the more basic moral good of pain.

This is not a strong assumption. Survival and reproduction do not trump all other moral goods, but they are usually better than the alternatives (death and infertility), in an all-things-considered sort of way.

Now, obviously, survival and reproduction are the key selection pressures in evolutionary history. So it would be unsurprising to find that evolved beings like ourselves have beliefs and desires that were correlated with them.

But since those selection pressures are in turn correlated with some moral truths (namely, that survival and reproduction are moral goods) we have an explanation of the puzzling coincidence between our normative beliefs and the mind-independent, causally inert moral truth.

In other words, what is evolutionarily beneficial has pre-established harmony with what is morally good, and what is evolutionarily beneficial causally shapes our cognitive faculties. This is, in effect, an inversion of Street's Darwinian Dilemma. It shows how robust realists have nothing to fear from evolutionary processes.

While you are digesting all of this, bear in mind that Enoch does not think that the correlation that needs to be explained is particularly impressive. So it does not matter if survival is not a primary or essential moral good. All that matters is that there is some slight correlation between normative beliefs and moral truths.


3. Too Good to be True?
Isn't this explanation just a little too convenient? Isn't there something fishy about it? For starters, why think that survival is a moral good?

Enoch offers a few responses. First, as noted above, it may be because it is itself correlated with other more basic moral goods, such as the absence of pain. Second, it may be true that some creatures are particularly evil and their continued existed would be bad. That, he thinks, does not really matter. As long as survival is good for creatures like us -- even if only because it makes other moral goods possible -- it is enough.

Maybe it is, but even so, hasn't Enoch just replaced one puzzling coincidence with another? I mean, isn't it somehow miraculous that evolutionary selection pressures just happened to align themselves with moral truths? This is a problem arising from the lack of counterfactual robustness inherent in Enoch's explanation: if things had been different...

Again, Enoch has a few responses. First, it is not clear that things could have been different. Could evolutionary processes really have aimed at something other than survival and reproduction?

Second, Enoch thinks it significant that he has reduced several puzzling coincidences -- between different normative beliefs and different moral truths -- to just one puzzling coincidence -- between the central evolutionary aim and a moral good. In the context of the plausibility game outlined above, this helps to raise realism's attractiveness.

Finally, brute luck is surely lurks behind other cognitive faculties that are shaped by evolutionary forces, e.g. those used in mathematical reasoning. So there is a level playing field when it comes to this issue.

4. Concluding Thoughts

So that's it; that's Enoch's solution to the epistemological challenge. He agrees that there are still concerns, but thinks his response can help to increase the plausibility of robust realism. In the final section of his article, he considers whether his solution could generalise to other contexts in which similar epistemological challenges are faced.

Unfortunately, he doesn't say very much. He says that its generalisability will depend on whether an analogue of the "goodness of evolutionary aims" can be found in other domains.

Maybe I can say a few words. As noted in part two, mathematical Platonism is the other theory that clearly faces a similar challenge. But, in some ways, I think the challenge may be easier to meet in that domain than it is in the case of morality.

Why do I think this? Well, I suppose I have in mind the fact that physical reality seems to be structured in a mathematical way. This is certainly the assumption underlying the science of physics. And since we have causal interactions with that physical reality, the fact that our mathematical beliefs line-up with mathematical truth is not particularly surprising.

Now there are gaps in this explanation. Certainly, the more abstruse aspects of number theory may have little connection with the physical structure of reality (I'll have to plead ignorance here). But that's not too worrying since, as Enoch noted, the correlation is relatively weak: not everyone is a good mathematician.

The question we need to consider is whether the response to the challenge in the case of mathematical Platonism is any better or worse than Enoch's response? It might be better in that the fact that evolutionary processes are subject to mathematical physical laws is less surprising than the fact (if it is a fact) that they are subject to moral laws. I certainly find the latter to be odder than the former, although I can't articulate the reason for my discomfort.

On the other hand, it may just be that I have found the analogy Enoch was alluding to.

Any thoughts?