Game Theory (Part 5) - Best Response and Expected Utility

Tweet

This post is part of my course on game theory. For an index, see here. The course follows the one by Ben Polak on the Open Yale website.

Over the past few entries we have been considering domination and the iterated deletion of dominated strategies. In today’s entry we move away from those concepts and begin our inexorable journey to the Nash Equilibrium. We do so by studying two key ideas: (i) best response and (ii) expected utility.



1. Best Response
Consider, for a moment, the following game. There is no story motivating its structure, so you’ll need to analyse it in the abstract.

The interesting thing about this game, for our purposes, is that it features no dominated strategies. This means we can’t utilise the method of iterated deletion when trying to solve it. So what can we do?

Well, we can appeal to the notion of best response. In other words, we can work out which strategies are the best responses for one player to the strategies of the other player. A strategy is a best response if it yields the highest possible payoff for one player, holding the other player’s choice of strategy fixed.

Looking at the game matrix above, and analysing it from the perspective of Player 1, we can say the following:

U is a best response to L. In other words, if Player 2 chooses L, then Player 1 does best by choosing U in response. 

M is a best response to R. In other words, if Player 2 chooses R, then Player 1 does best by choosing M in response. 

D is neither a best response to R or to L. However, it does better than M against L and better than U against R.

We can perform a similar analysis from the perspective of Player 2. This would show that L is a best response to M, and R is a best response to U and D.



2. Expected Utility
That seems straightforward enough, but how useful is this information? One obvious problem is that whether a strategy is a best response or not depends entirely on what you think the other player is doing. And since you usually face some uncertainty or doubt about what the other player is going to do, this means you have to incorporate probabilities into your analysis.

If probabilities have to be incorporated into the analysis of a game, then we are confronted with the notion of expected utility. The expected utility of a payoff is the payoff attached to a particular outcome multiplied by some relevant probability. In game theory, the relevant probabilities are assumptions or beliefs about what the other player(s) are going to do.

Looking back once more to the game matrix given above, let’s assume that we are Player 1 and we believe Player 2 switches between his strategies with probability (0.5, 0.5). In other words, he plays L half of the time and R half of the time. This affects how we calculate our expected payoffs in the following manner:

The Expected Utility of:

• U vs. (0.5, 0.5) = (0.5)(5) + (0.5) (0) = 2.5

• M vs. (0.5, 0.5) = (0.5)(1) + (0.5)(4) = 2.5

• D vs. (0.5, 0.5) = (0.5)(4) + (0.5)(2) = 3

Notice anything interesting about this? All of sudden, D has become the best response. Of course, this is only because of the specific probabilities we attached to Player 2’s strategies. It could be that 2 switches between his strategies with probability (1/3, 2/3) or (2/3, 1/3). Indeed, there are a potentially infinite number of different probability combinations.



3. Expected Utility and Best Response
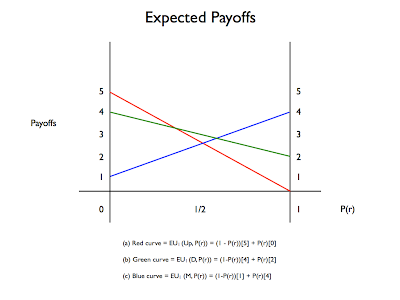
It would be impossible to work our way through all of these different combination in the same manner as we did for the combination (0.5, 0.5). So is there any other way we can work out the best response for player 1 to all possible probability combinations of player 2? Yes there is: by drawing the following picture.

As you can see, this picture depicts the expected utility for each strategy of Player 1 (U, M, D) against every possible probability combination of Player 2’s strategies (p, 1-p). We can now use this graph to work out all of Player 1’s best responses. As in the following diagram.

This diagram shows that for all probability combinations to the left of x, U is Player 1’s best response; for all probability combinations to the right of y, M is Player 1’s best response; and for all probability combinations between x and y, D is Player 1’s best response.

This seems like useful information, and it can be made even more useful by solving for x and Y. Here’s how you would solve for x:

1) Replace p(R) with x in your expected utility calculations e.g. 

• Expected Utility (EU) of (D, p(R)) = (1-x) (4) + x(2)
• Expected Utility (EU) of (U, p(R)) = (1-x) (5) + x(0)

2) Set the EU equations for D and U equal to each other. Why? Because, looking back to our diagram, these two lines intersect at x. The resulting calculation looks like this: 

• (1-x)(4) + x(2) = (1-x)(5) + x(0) 
• 4 - 4x + 2x = 5 - 5x 
• 3x = 1 
• x = 1/3

You can follow a similar procedure when solving for y, just set the the EU-equations for D and M equal to each other.

Okay, that’s all for today. In the next entry we’ll look at penalty kicks.